U pohovorů na pozici výzkumníka v Seznamu se ptávám na principy vybraných algoritmů strojového učení, mezi které patří i k-means pro shlukování. Po tom, co algoritmus dáme dohromady, následuje otázka, zda je zaručené, že algoritmus vždy skončí. Tušil jsem, že se dají najít extrémní případy, kdy algoritmus může začít nekonečně dlouho kmitat mezi několika stejně dobrými řešeními, a tak jsem požadoval drobné doplnění ukončovací podmínky (například detekci cyklu), která by ukončení garantovala.
Nedávno jsem však narazil na uchazeče, který byl skálopevně přesvědčený, že standardně definovaný k-means skončí za všech okolností a přísnější kritérium není potřeba. Vzhledem k tomu, že jsem žádný protipříklad připravený neměl, zkusil jsem nejprve zahledat na internetu. A ejhle. Internet je plný „důkazů“ toho, že k-means konverguje. Tvrdí to dokonce i Wikipedie! Nezbylo mi tedy nic jiného, než ten protipříklad vymyslet. Tady je.
Algoritmus k-means
K-means patří do skupiny takzvaných algoritmů strojového učení bez učitele. Jeho cílem je nalezení k shluků daných bodů, kde shlukem rozumíme skupinu bodů, které jsou si navzájem blízko (ve smyslu nějaké metriky). Typickým příkladem použití může být analýza zákazníků internetového obchodu, které chceme podle zájmů a chování roztřídit do předem neznámých kategorií.
Vstupem algoritmu je množina m bodů, které jsou definované souřadnicemi v n-rozměrném prostoru, a číslo k, určující požadovaný počet shluků. Všechny shluky jsou reprezentované svými středy a každý bod potom náleží do shluku, jehož střed je mu nejblíže. Souřadnice středů se určují iterativním způsobem založeným na EM algoritmu. Zde uvádím jeho neformální zápis (zájemci o preciznější definici si ho můžou nastudovat na příklad na Wikipedii):
- Pro každý shluk zvol náhodně souřadnice jeho středu (typicky se volí totožně se souřadnicemi náhodně vybraných různých bodů).
- Každý bod přiřaď středu, ke kterému leží nejblíže.
- Urči nové souřadnice středů jako průměr souřadnic všech bodů, které náleží do daného shluku.
- Opakuj od bodu 2, dokud se shlukování neustálí.
Princip algoritmu je ilustrovaný obrázkem 1.
Není obtížné dokázat, že tento iterativní algoritmus neustále zmenšuje chybu, definovanou jako součet vzdáleností všech bodů od středů svých shluků, a spěje tak k nějakému lokálně-optimálnímu řešení. Co však, pokud dojde k tomu, že má jeden bod stejně daleko ke středům dvou nebo více různých shluků? V takovém případě je možné náhodně vybrat libovolný z nich a v tom je kámen úrazu.
Protipříklady
Začněme velmi jednoduchým příkladem. Mějme pouze dva body, které leží přesně na sobě, a hledejme 2 shluky. Pokud budou jejich středy inicializovány do stejného místa jako shlukované body, máme problém, neboť v kroku 2 algoritmu bude mít každý bod stejně daleko ke dvěma středům, a může si tak vybrat odlišný od toho z předchozí iterace. Tím se změní shlukování a algoritmus tak pokračuje dál. Takto je možné kmitat mezi čtyřmi řešeními libovolně dlouho a algoritmus nemusí nikdy skončit.
Dalo by se namítnout, že se v tomto jednoduchém příkladu oba shluky překrývají a nemuseli bychom je tedy považovat za různá řešení. Lze však vymyslet i netriviální příklady.
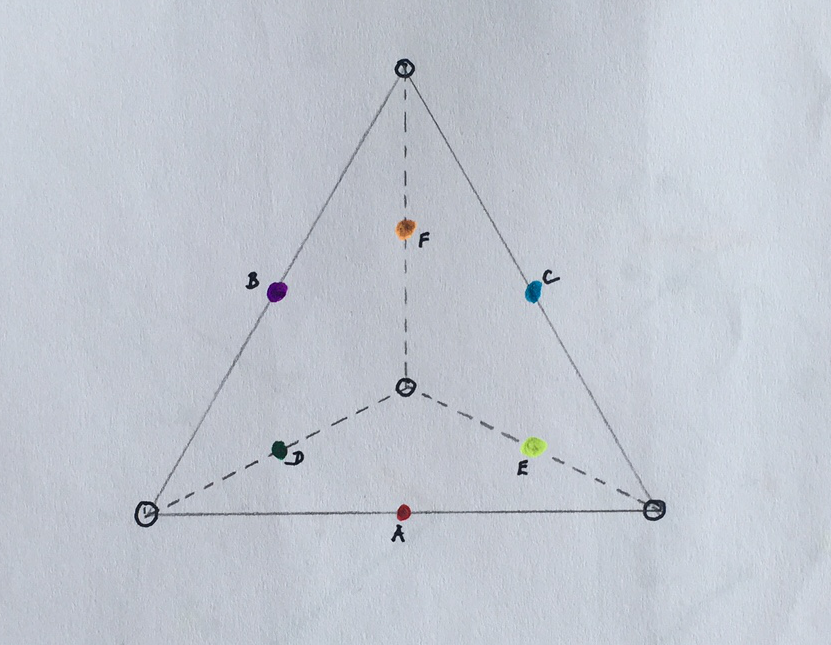
Mějme 10 bodů v trojrozměrném prostoru, které leží na vrcholech a v polovinách středů hran pomyslného pravidelného čtyřstěnu, a hledejme 6 shluků, jejichž středy A, B, C, D, E, F jsou inicializovány do středů hran, jak je ilustrováno na obrázku 2.
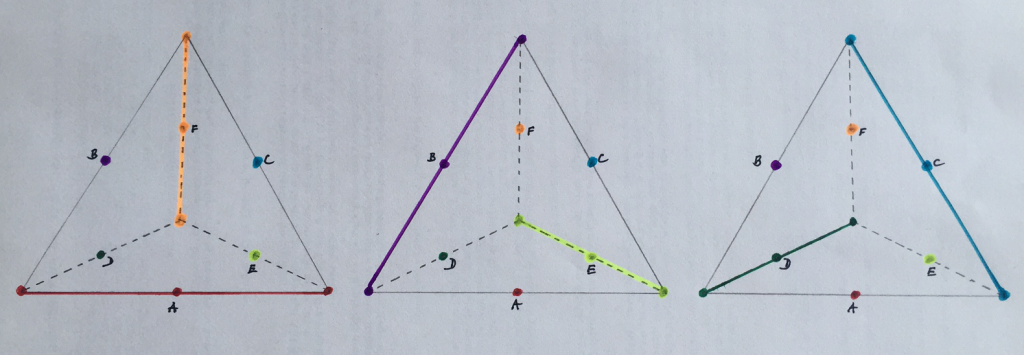
V takovém případě jsou vždy body na vrcholech stejně daleko od tří různých středů a je možné je tedy přiřadit třem různým shlukům. Existují tři různá shlukování, mezi kterými může algoritmus kmitat, aniž by zkonvergoval. Tato různá řešení jsou znázorněna na obrázku 3.
Klasický algoritmus k-means tedy v extrémních případech konvergovat nemusí. Opatření, která jeho skončení zajistí jsou však snadná. Nejjednodušším z nich je determinizace výběru shluku v případě, že máme více možností. Shluky si můžeme očíslovat a místo náhodného výběru vybírat například vždy ten s nejnižším identifikátorem. Jinou možností je detekovat kmitání nebo změnit ukončovací podmínku algoritmu a zastavit v případě, že už se chyba shlukování nezmenšuje. Nic takového však standardní definice algoritmu neuvádějí a tvrzení, že k-means vždy konverguje je tedy nesprávné.