U pohovorů na pozici výzkumníka v Seznamu se ptávám na principy vybraných algoritmů strojového učení, mezi které patří i k-means pro shlukování. Po tom, co algoritmus dáme dohromady, následuje otázka, zda je zaručené, že algoritmus vždy skončí. Tušil jsem, že se dají najít extrémní případy, kdy algoritmus může začít nekonečně dlouho kmitat mezi několika stejně dobrými řešeními, a tak jsem požadoval drobné doplnění ukončovací podmínky (například detekci cyklu), která by ukončení garantovala.
Nedávno jsem však narazil na uchazeče, který byl skálopevně přesvědčený, že standardně definovaný k-means skončí za všech okolností a přísnější kritérium není potřeba. Vzhledem k tomu, že jsem žádný protipříklad připravený neměl, zkusil jsem nejprve zahledat na internetu. A ejhle. Internet je plný „důkazů“ toho, že k-means konverguje. Tvrdí to dokonce i Wikipedie! Nezbylo mi tedy nic jiného, než ten protipříklad vymyslet. Tady je.
Algoritmus k-means
K-means patří do skupiny takzvaných algoritmů strojového učení bez učitele. Jeho cílem je nalezení k shluků daných bodů, kde shlukem rozumíme skupinu bodů, které jsou si navzájem blízko (ve smyslu nějaké metriky). Typickým příkladem použití může být analýza zákazníků internetového obchodu, které chceme podle zájmů a chování roztřídit do předem neznámých kategorií.
Vstupem algoritmu je množina m bodů, které jsou definované souřadnicemi v n-rozměrném prostoru, a číslo k, určující požadovaný počet shluků. Všechny shluky jsou reprezentované svými středy a každý bod potom náleží do shluku, jehož střed je mu nejblíže. Souřadnice středů se určují iterativním způsobem založeným na EM algoritmu. Zde uvádím jeho neformální zápis (zájemci o preciznější definici si ho můžou nastudovat na příklad na Wikipedii):
- Pro každý shluk zvol náhodně souřadnice jeho středu (typicky se volí totožně se souřadnicemi náhodně vybraných různých bodů).
- Každý bod přiřaď středu, ke kterému leží nejblíže.
- Urči nové souřadnice středů jako průměr souřadnic všech bodů, které náleží do daného shluku.
- Opakuj od bodu 2, dokud se shlukování neustálí.
Princip algoritmu je ilustrovaný obrázkem 1.
Není obtížné dokázat, že tento iterativní algoritmus neustále zmenšuje chybu, definovanou jako součet vzdáleností všech bodů od středů svých shluků, a spěje tak k nějakému lokálně-optimálnímu řešení. Co však, pokud dojde k tomu, že má jeden bod stejně daleko ke středům dvou nebo více různých shluků? V takovém případě je možné náhodně vybrat libovolný z nich a v tom je kámen úrazu.
Protipříklady
Začněme velmi jednoduchým příkladem. Mějme pouze dva body, které leží přesně na sobě, a hledejme 2 shluky. Pokud budou jejich středy inicializovány do stejného místa jako shlukované body, máme problém, neboť v kroku 2 algoritmu bude mít každý bod stejně daleko ke dvěma středům, a může si tak vybrat odlišný od toho z předchozí iterace. Tím se změní shlukování a algoritmus tak pokračuje dál. Takto je možné kmitat mezi čtyřmi řešeními libovolně dlouho a algoritmus nemusí nikdy skončit.
Dalo by se namítnout, že se v tomto jednoduchém příkladu oba shluky překrývají a nemuseli bychom je tedy považovat za různá řešení. Lze však vymyslet i netriviální příklady.
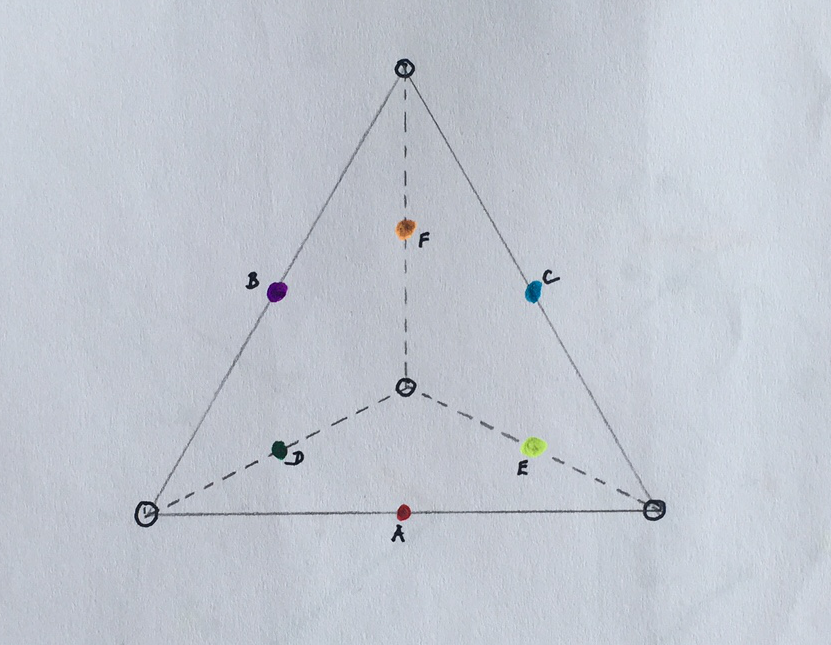
Mějme 10 bodů v trojrozměrném prostoru, které leží na vrcholech a v polovinách středů hran pomyslného pravidelného čtyřstěnu, a hledejme 6 shluků, jejichž středy A, B, C, D, E, F jsou inicializovány do středů hran, jak je ilustrováno na obrázku 2.
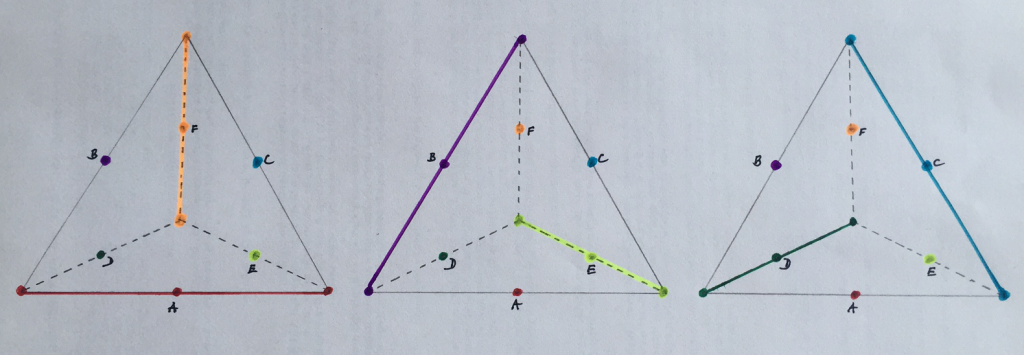
V takovém případě jsou vždy body na vrcholech stejně daleko od tří různých středů a je možné je tedy přiřadit třem různým shlukům. Existují tři různá shlukování, mezi kterými může algoritmus kmitat, aniž by zkonvergoval. Tato různá řešení jsou znázorněna na obrázku 3.
Klasický algoritmus k-means tedy v extrémních případech konvergovat nemusí. Opatření, která jeho skončení zajistí jsou však snadná. Nejjednodušším z nich je determinizace výběru shluku v případě, že máme více možností. Shluky si můžeme očíslovat a místo náhodného výběru vybírat například vždy ten s nejnižším identifikátorem. Jinou možností je detekovat kmitání nebo změnit ukončovací podmínku algoritmu a zastavit v případě, že už se chyba shlukování nezmenšuje. Nic takového však standardní definice algoritmu neuvádějí a tvrzení, že k-means vždy konverguje je tedy nesprávné.




https://en.m.wikipedia.org/wiki/K-means_clustering
Pakliže bod 4 bude: Opakuj dokud se pozice středů nezmění, tak uvedené protipříklady nebudou fungovat.
Pokud se na středy budete dívat jako na množinu vzájemně nerozlišitelných bodů, tak máte pravdu. Každý střed je ale určený svými body, které reprezentuje. Ty se v tom protipříkladu mění, takže se formálně jedná o různé středy, přestože leží na stejném místě.
To je pravda, určitě záleží na definici. Třeba zde http://nlp.stanford.edu/IR-book/html/htmledition/k-means-1.html je k-means definován tak, že se jedná o množinu nerozlišitelných bodů a určitě existuje i mnoho jiných referencí, který ukazí na jinou implementaci. Napadá vás příklad, v kterém by definice s nerozlišetelnou množinou bodů byla znevýhodněna oproti té druhé?
Řekl bych, že ve většině praktických aplikací chceme, aby jednotlivé body byly rozlišitelné -- jsou to lidé, transakce, dokumenty apod. Podle toho, do jakého clusteru spadnou se s nimi dále pracuje.
Díky za vysvětlení. Jinak, těším se na další příspěvky blogu!
Moc zajímavé téma, díky za pěkný článek. Ale poukázal bych na jeden podstatný aspekt: asi bychom měli rozlišovat mezi 1) algoritmem; a 2) implementací algoritmu v konkrétním výpočetním prostředí a datových strukturách (možná to není úplně ideální rozlišení, ale teď pracovně stačí). Zde to chápu tak, že (1) je formální záznam logicko-symbolických operací nad množinovým universem (tzn. je to atemporální proces, podobně jako třeba průběh funkce je atemporální - funkce nikam "neběží", ona prostě je, vždycky byla a bude, jen jsem ji svým zápisem pojmenoval), zatímco (2) je temporální proces nad konkrétními objekty, které existují v čase a prostoru.
U (1) tedy plně platí princip extenzionality: pokud dvě množiny obsahují zcela stejné prvky, pak to správně nejsou dvě množiny, ale jedna a táž množina, pouze se dvěma jmény. Stejně tak pokud budu mít v matematicky definovaném stavovém prostoru x1 = [1; 2], x2 = [1; 2], tak ať chci, nebo ne, x1 = x2, a jde tudíž o bod jediný, nikoli o dva body ve vzájemném zákrytu. A stejně tak vzpomeneme-li strašlivě otřepaný ;-) leč stále velmi fungující učebnicový příklad Jitřenky a Večernice: nejsou to dvě různé hvězdy, jejichž poloha je (shodou okolností) v neustálém zákrytu. Čili to, co mi odlišuje Jitřenku, Večernici a Venuši, je až intenze, neboť extenzionálně jde o tentýž objekt.
U (2) si pak samozřejmě dovedu představit, že v praktickém aplikovaném případě mám kolekci dokumentů (nebo zákazníků, nebo čehokoli), kdy se mi dva nebo více dokumentů zobrazí do jediného bodu ve stavovém prostoru (např. při bag of words, ale to musí asi být zatraceně náhoda? to spíš ti zákazníci mají tendenci padat v relativně nízkorozměrných prostorech do stejných bodů). Pak je samozřejmě aplikačně zcela oprávněné očekávat, že když takovouto množinu dokumentů nasypu do nějakého out-of-the-box k-means algoritmu, dostanu v konečném čase rozumnou odpověď a neuvíznu v takovém nekonečném cyklu, který je popsán výše v článku. Přísně vzato pak ale vzhledem k "vanilla k-means" algoritmu dělám chybu já, nikoli ten algoritmus sám, že nehlídá nekonečné cykly vzniklé vícenásobným zahrnutím identického geometrického bodu do vstupních dat (ostatně asi by měl na ta vstupní data aplikovat distinct). To, že záměrně *chci* ponechat některé identické body ve vstupních datech vícekrát, je otázkou intenze, skrze níž já vidím ten řešený problém (a samozřejmě i otázkou intence :-) ), ale která není obsažena v původně extenzionální definici algoritmu.
Takže já osobně bych asi byl toho názoru, že extenzionální k-means (1) konverguje vždy (ale nemám to už dál rozmyšlené, možná fakt budou nějaké další protipříklady...), zatímco intenzionální k-means (2) může mít kdejaké nečekané zášlehy a je potřeba ho víc ohlídat.
Jak nakonec dopadl u pohovou ten kandidát, který trval na tom, že standardně definovaný k-means konverguje vždy? :-)
Díky za pěkný a rozsáhlý komentář. Toho kandidáta jsme nakonec nevzali, ale to, že trval na konvergenci v tom žádnou roli nehrálo. U pohovoru mě zajímá, jak člověk přemýšlí, ne jaká fakta zná nebo jim věří:)
Ano, konvergence neni ganrantovana (napriklad ale greedy alg by mel konvergovat, nicmene to opravdu neni bezna implementace), take je to NP hard, a ani neni garantovana deterministicnost algoritmu (citlivy na pocatecni podminky). Obecne se jedna o optimizacni ulohu.
Ale spis si ale myslim, ze k-means lide neuvazuji bez "stop" podminek, kde najdeme alespon lokalni optimum :-)
Základem problému je, že otázka je špatně položená. Problém je v definici "algoritmu" jak je napsaná v článku. Nejde totiž o algoritmus ale pseudoalgoritmus neobsahující důležité detaily, které musí být v algoritmu dořešené. Můj oblíbený citát od Donada Knutha říká: Algorithm must be seen to be believed.
Takže pokud se budeme bavit o K-Means jako pseudoalgoritmu, který má tisíc různých variací (některé horší než jiné), pak konvergovat nemusí. Pokud se bavíme o konkrétních algoritmech, které jsou naimplementovány v ML knihovnách, pak K-Means vždy konverguje (jinak autor něco podcenil).
K příkladu 1. Popravě nevím, jestli by tady má knihovna konvergovala a radši to ověřím. Problém je v tom, že řeším i problém s prázdnými shluky, t.j. oba body by se dostaly do jednoho shluku ale možná by se pak jeden bod přiřadil k prázdnému shluku a tím by algoritmus nekonvergoval. V reálu to není problém, protože bodů je mnohem více než shluků a jen zlomek jsou identické body.
K příkladu 2. Algorimuts by konvergoval i kdyby se body přiřazovaly náhodně. Ano, s nenulovou pravděpodobností bude nekonečně kmitat v uedených konstelacích, ale tato pravděpodobnost jde extrémně rychle k nule.
Pokud chcete další zábavnou otázku na pohovor týkající se K-Means, tak se zeptejte, zda bude algoritmus fungovat při maximalizaci cosinové podobnosti místo minimalizace Eukleidovské vzdálenosti (upravený 2. krok)...